共计3539个字符,预计需要花费9分钟才能阅读完成。
什么是神经网络?
首先我们来看百度对神经网络的定义:
人工神经网络(Artificial Neural Network,即 ANN),是 20 世纪 80 年代以来人工智能领域兴起的研究热点。它从信息处理角度对人脑神经元网络进行抽象,建立某种简单模型,按不同的连接方式组成不同的网络。在工程与学术界也常直接简称为神经网络或类神经网络。神经网络是一种运算模型,由大量的节点(或称神经元)之间相互联接构成。每个节点代表一种特定的输出函数,称为激励函数(activation function)。每两个节点间的连接都代表一个对于通过该连接信号的加权值,称之为权重,这相当于人工神经网络的记忆。网络的输出则依网络的连接方式,权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近,也可能是对一种逻辑策略的表达。
顾名思义,神经网络就是尝试模拟大脑神经元的工作,完成完成信息处理和模式识别等任务,如图像识别,语音识别等等。这些任务对大脑而言是显而易见的,但在计算机科学和机器学习领域,却是非常复杂和具有挑战性的。因为没有一个程序能直接编写出模拟神经元的复杂功能,因此研究人员通过设计和训练神经网络来近似模拟这些功能。
神经网络是如何进行识别的?
为了说明这个问题,我们引入猫狗分类(即 二分类)这种简单的问题,看看它是如何工作的。
这里有两张黑白的猫狗图片,它们的像素 256×256,想象一下你的大脑是如何分辨这两张图片。


首先,大脑会通过视觉感知来识别图像的不同特征,比如猫的耳朵和胡须,狗的鼻子和嘴巴等。根据这些特征,大脑会给出猫或者狗的相似度(一个值:0%~100%),最终给出我们的判断:是猫还是狗。
同理,神经网络也应该具有类似的结构,能够提取和识别图像特征,并最终给出各种分类的相似度(在本例中只有两类,即猫或者狗)。
接着我们给出猫狗识别的简单的神经网络结构(这里采用的是全连接神经网络FCNN,而并非CNN)。
如果你曾经了解过神经网络,你应该对下面的图很熟悉。

但如果你是第一次见,也没关系,我将以猫狗识别为例子,解释这张图每一项的具体含义。
首先,我们将图片展开,将图片的每一行拼接到一起,形成了 256*256=65536 个像素点组成的列,我们称该列中的每个元素为一个 神经元 ,并称该列为 输入层(即输入图片的数据)。

很明显,它共有 256*256=65536 个神经元,可以暂时将它想象成我们眼睛的感光细胞,向我们大脑传输了最原始图片信息。现假设每个神经元有一个范围为 0.0~1.0 的感光数据(神经元的数据称为 激活值),代表该像素点的亮度值,越接近 1.0 说明该像素点越亮,反之越暗。
为了识别该图片是猫还是狗,大脑会识别各种特征,如该动物的眼睛,鼻子,耳朵等等。因此我们还需要 隐藏层(可以不止一层,这里为了方便从一层讲起),用于模仿大脑识别图片的各种特征。

如上图所示,同样为了方便,我们只为隐藏层的设定三个神经元,假设其分别代表三个特征的相似度:狗的耳朵、猫的耳朵和猫的眼睛(在真实的神经网络中,往往是黑箱模型,即我们并不知道哪个神经元对应了哪些特征)。
根据隐藏层神经元的相似度值,我们就能计算出猫和狗的概率。拥有越多猫的特征,那么其越可能是猫,反之为狗。这里是二分类问题,因此我们通常使用 softmax 函数 将输出概率控制到 0.0~1.0 区间内,方便判断。上图所示的输出中,有 0.9 的概率为猫,有 0.1 的概率为狗。
那么这些线又是干啥的呢?

这些线代表了上一层数据的流向,即下一层的数据是根据哪些上层数据计算得来的。
用数学表达式来描述神经网络结构
看完上一章节,想必你已经了解了神经网络的大致原理和结构,那么我们现在来讨论一下每一层神经元的值是如何得到的。此外,在本章节我们还要讨论如何用数学表达式来描述该结构。
注意:本章节需要用到线性代数的知识,如果不知道矩阵是什么,那还是先去百度上了解一下吧。
输入层到隐藏层神经元激活值的计算
我们假设输入层的神经元激活值分别为 x_1,x_2,x_3,\cdots,x_{65535},则可以用矩阵:
X=
\begin{pmatrix}
x_1 & x_2 & x_3 & \cdots & x_{65535} \\
\end{pmatrix}其中 X 表示输入的值。
同理,又输入层变换得到的隐藏层的所有激活值可表示为矩阵:
H=
\begin{pmatrix}
h_1 & h_2 & h_3 \\
\end{pmatrix}
图中的每一条线都代表乘以一个 权重(Weight),如w_{11}。那么隐藏层第一个神经元的激活值可以由以下公式计算:
h_0=w_{1,1}*x_0+w_{2,1}*x_1+w_{3,1}*x_2+\cdots+w_{65536,1}*x_{65535}为了保证数值尽量在 0.0~1.0(为了方便计算)之间,我们还引入了 偏差 (Bias),如 $$b_1$$。同时再加上激活函数,这里采用Sigmoid,用\sigma(x) 表示:
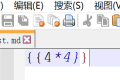
\sigma(x)=\frac{1}{1+e^{-x}}此时:
h_0=\sigma(w_{1,1}*x_0+w_{2,1}*x_1+w_{3,1}*x_2+\cdots+w_{65536,1}*x_{65535}+b_1)那么对于所有的 h_i(i=1,2,3) 如何表示呢?聪明的你肯定发现了,可以用矩阵来表示 权重 (W) 和偏差(B):
W=
\begin{pmatrix}
w_{1,1} & w_{1,2} & w_{1,3} \\
w_{2,1} & w_{2,2} & w_{2,3} \\
\vdots & \vdots & \vdots \\
w_{65536,1} & w_{65536,2} & w_{65536,3} \\
\end{pmatrix}B=
\begin{pmatrix}
b_1 & b_2 & b_3 \\
\end{pmatrix}好了,很明显,由矩阵的乘法我们可以得到:
H=\sigma(X \cdot W + B)这样我们就完美的解决了输入层到隐藏层激活值的计算问题。
每一层之间的公式关系
根据输入层到隐藏层之间的公式关系,我们可以仿照着推出隐藏层到输出层之间的关系。

设输出的两个值 y_0,y_1 分别代表该图片的动物是猫和是狗的概率(显然概率范围在 0.0~1.0 之间),我们用矩阵表示:
Y=
\begin{pmatrix}
y_0 & y_1 \\
\end{pmatrix}在这里为了保证 y_0,y_1 在 0.0~1.0 之间,我们采用softmax 函数,引入权重和偏差,则:
Y=softmax(W' \cdot H + B')其中权重和偏置分别为:
W'=
\begin{pmatrix}
w_{1,1} & w_{1,2} \\
w_{2,1} & w_{2,2} \\
w_{3,1} & w_{3,2} \\
\end{pmatrix}B'=
\begin{pmatrix}
b_1 & b_2 & b_3 \\
\end{pmatrix}那么我们此时就得到了从输入层到输出层的完整函数表达式:
Y=softmax(W' \cdot \sigma(X \cdot W + B) + B')权重和偏差的确定和意义
根据上述的公式,我们给出输入的图片,就能得到输出猫或者狗的概率。要保证输出结果的正确性,那么必须确定参数 W,B,W',B'。
我们要知道,确定神经网络中的权重和偏差是一项至关重要的任务,因为这些参数直接影响模型的性能和准确度。通常,这些参数是通过一种称为 训练(training) 的过程来确定的。在这个过程中,我们使用大量的已知标签(如已知是猫或狗的图片)来调整网络的参数,使得网络的输出尽可能接近实际标签。
这些调整的过程通常涉及到以下几个步骤(在这里由于只是介绍,就不在过多赘述,将在以后的章节中详细解释):
-
前向传播(Forward Propagation)
前向传播是指从输入层开始,通过隐藏层,直到输出层的计算过程。在每一层中,神经元的激活值会被计算出来,并传递到下一层,直到最终得到输出。 -
损失函数(Loss Function)
损失函数用来衡量模型的预测值与实际值之间的差异。在猫狗分类问题中,常用的损失函数是交叉熵损失(Cross-Entropy Loss)。 -
反向传播(Backpropagation)
反向传播是调整权重和偏差的关键步骤。通过计算损失函数相对于每个参数的梯度,我们可以知道如何调整这些参数以减少损失。具体来说,反向传播使用链式法则(Chain Rule)来计算梯度,然后根据这些梯度更新参数。更新规则通常是使用梯度下降算法(Gradient Descent Algorithm)。 -
梯度下降算法(Gradient Descent Algorithm)
梯度下降算法是通过迭代来逐步优化损失函数。具体来说,它会计算每个参数的梯度,然后沿着梯度的反方向更新参数,以减小损失。